子集型回溯
在一次 dfs函数里面，如果 path 是 mutable 类型, 一定保证path进入函数和出函数时 状态一定不变。不管有多少个分支，每个分支都要考虑这个问题。
如果 path是immutable，如string，它作为参数传递给dfs，这种情况下根本没有在修改它的状态，而是每次新建一个string，传给子节点。因而不需要恢复状态。LC 257.
模版一：选或不选
从输入的角度思考
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution: #LC78题子集
def subsets(self, nums: List[int]) -> List[List[int]]:
path=[]
res=[]
def dfs(i):
if i==len(nums):
res.append(path.copy())
return
#选择这个
path.append(nums[i])
dfs(i+1)
#不选这个
path.pop()
dfs(i+1)
dfs(0)
return res
|
path.copy()的时间复杂度为O(N), 总体时间复杂度(N*2^N).
求子集的这种做法，一定等到i=n时，遍历完所有元素才添加答案。
LC 90
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
n=len(nums)
res=[]
path=[]
nums.sort()
def dfs(i):
if i==n:
res.append(path.copy())
return
#选
path.append(nums[i])
dfs(i+1)
path.pop()
#不选
if len(path)==0 or (len(path)>0 and path[-1]!=nums[i]):
dfs(i+1)
dfs(0)
return res
|
以 111 为例，检查当前 path，只有 path 中最后一个元素与当前元素不相等时，才可以不选当前元素。换句话说，如果两个相同的数字挨在一起，并且选了第一个数字，那就也必须选第二个数字。
因为会有00，01,10,11四种可能，表示选或者不选相邻的两个相同元素（比如 2），这样操作可以去掉第三种情况，最后得到的结果是[],[2],[22].
LC 491🌟
输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution:
def findSubsequences(self, nums: List[int]) -> List[List[int]]:
n=len(nums)
res=[]
path=[]
def dfs(i, cur):
if i==n:
if len(path)>=2:
res.append(path.copy())
return
#选
if nums[i]>=cur:
path.append(nums[i])
dfs(i+1, nums[i])
path.pop()
#不选
if len(path)==0 or (len(path)>0 and cur!=nums[i]):
dfs(i+1, cur)
dfs(0, -101)
return res
|
与90题的不同在于，相同的数字不一定相邻，比如1，10，1，1。这种情况就无法用模版二。
模版二：从答案的角度思考
考虑当前问题和子问题,每个节点都是一个答案。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res=[]
path=[]
def dfs(i):
res.append(path.copy())
if i==len(nums):
return
for j in range (i, len(nums)):
#随便找一个数加进去
path.append(nums[j])
#必须得从它后面再找数加进去
dfs(j+1)
path.pop()
dfs(0)
return res
|
LC 90 Subset II
[1,2,2]找子集,但是[1,2]只能出现一次。
使用模板二，树的某一层中，不能有重复的节点。模版2️⃣的某一层实际上就是 for 循环，只需要在 for 循环里面检查当前选的元素被选了没有。（画图理解）
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution:
def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
nums.sort()
n=len(nums)
path=[]
res=[]
def dfs(i):
res.append(path.copy())
if i==n:
return
for j in range(i, n):
if j>i and nums[j]==nums[j-1]:
continue
path.append(nums[j])
dfs(j+1)
path.pop()
dfs(0)
return res
|
LC 39 组合总和
输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
注意递归终点一定需要加上target<0, 否则无限循环。
用模版一亦可。
类似题目：377. 组合总和 Ⅳ. 这题的不同是[2,2,3]和[2,3,2]可以作为两个答案
二叉树回溯
二叉树回溯与普通回溯的区别在于，不能在边界条件把答案加入res. 因为一个leaf，对它的两个子节点判断root==null, 则会把答案加进 res两次。一般在判断是叶子节点之后加入 res. LC 113
二叉树回溯最好把path作为参数传递。
LC 257 二叉树的所有路径
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| #2025-02-04
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
path=''
res=[]
def dfs(root,path):
if not root:
return
path+=str(root.val)
#当前节点如果不是leaf, 加入->
if root.left!=root.right:
path+="->" # 这里实际上是新建一个path
#如果是 leaf，加入答案
else:
res.append(path)
dfs(root.left, path)
dfs(root.right, path)
dfs(root,path)
return res
|
path是个immutable，作为参数在传递. 不需要考虑状态恢复。
LC 437
给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
#cnt数组记录当前节点到根节点的所有路径和，以及它们的个数
cnt=defaultdict(int)
cnt[0]=1 #preSum[0]=0
res=0
def dfs(root, s):
nonlocal res
if not root:
return
s+=root.val
res+=cnt[s-targetSum]
cnt[s]+=1
dfs(root.left, s)
dfs(root.right, s)
cnt[s]-=1
dfs(root, 0)
return res
|
组合型回溯
与子集型回溯的不同是，path是定长的。
模版一
递归树是一颗二叉树，每个分叉是选/不选
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution: #LC 22
def generateParenthesis(self, n: int) -> List[str]:
# 2n个位置里面，选n个位置放左括号。组合型回溯，模版一
path=[]
res=[]
m=2*n
# open用来记录左括号的数量。只要open<n, 就可以选左括号
# 右括号的数量为i-open. 只有i-open<open, 才能选右括号
def dfs(i, open):
if i==m:
res.append(''.join(path))
return
#选左括号
if open<n:
path.append('(')
dfs(i+1, open+1)
path.pop()
#选右括号
if i-open<open:
path.append(')')
dfs(i+1, open)
path.pop()
dfs(0, 0)
return res
|
模板二
与子集型回溯的模版二类似，答案是选出递归树的某一层。递归树是一颗多叉树，每个分支代表选从起点 i开始的一个数字。
剪枝: 当前 path还需要m个数，但是剩余可选的数字数量<m
时间复杂度：叶子数量✖️根到叶子的长度，也就是C(n,k)*k
空间复杂度：O(k)
LC 216 Path Sum III
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| class Solution:#模版二
def combinationSum3(self, k: int, n: int) -> List[List[int]]:
path=[]
res=[]
def dfs(i, target):
#剪枝1: 还需要m个,剩余可选的的不够 m
m=k-len(path)
if m>10-i:
return
#剪枝2: 现在的路径和已经超过了 target
if target<0:
return
#剪枝3: 即使全部选最大的数，还是不够 target
#从 9开始选m个最大的数
if (9+9-m+1)*m<target*2:
return
if len(path)==k:
if target==0:
res.append(path.copy())
return
for j in range(i, 10):
path.append(j)
dfs(j+1, target-j)
path.pop()
dfs(1, n)
return res
|
排列型回溯
LC 47
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution:
def permuteUnique(self, nums: List[int]) -> List[List[int]]:
path=[]
res=[]
n=len(nums)
used=[False]*n
def dfs():
if len(path)==n:
res.append(path.copy())
return
for i, x in enumerate(nums):
if not used[i]:
if i>0 and x==nums[i-1] and not used[i-1]:
print(x)#如果轮到x'进，但是x没用过，输出
continue
used[i]=True
path.append(x)
dfs()
used[i]=False
path.pop()
nums.sort()
dfs()
return res
|
全排列需要一个数组来记录某个元素是否在 path上被用过。
以[1,1’,2]为例，在for循环上遍历到1’，但是发现1还没有用过时，直接退出递归，就是我画圈的两个地方。最后从控制台输出也可以看出，输出了两遍 1.
LC 51. N皇后
维护一个数组，记录每一行皇后的index. 再用一个set记录当前可以用的列数。每次递归，mark一下用过的index（列号）。
两个皇后在同一斜线上：他们的行列之和/之差相等。
以 111 为例，检查当前 path，只有 path 中最后一个元素与当前元素不相等时，才可以不选当前元素。换句话说，如果两个相同的数字挨在一起，并且选了第一个数字，那就也必须选第二个数字。
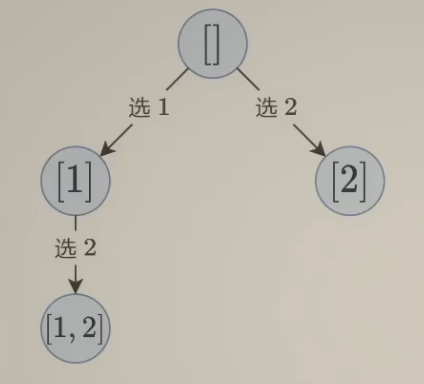
以[1,1’,2]为例，在for循环上遍历到1’，但是发现1还没有用过时，直接退出递归，就是我画圈的两个地方。最后从控制台输出也可以看出，输出了两遍 1.